Matematika Model
Gambar 1. Model control pada mesin penukar kalor [1]
Pendahuluan
Hasil utama dari pengembangan model matematis dari sistem teknik kimia adalah pemahaman yang diperoleh tentang apa yang benar-benar membuat proses “berjalan”. Wawasan ini memungkinkan untuk melepaskan dari masalah banyak “faktor kebingungan” asing guna mendapatkan inti dari sistem sehingga hubungan sebab-akibat antara variabel dapat lebih jelas. Model matematika berguna dalam semua fase teknik kimia, mulai dari penelitian dan pengembangan hingga operasi pabrik, dan bahkan dalam studi bisnis dan ekonomi.
- Penelitian dan pengembangan: menentukan mekanisme dan parameter kinetika kimia dari data reaksi laboratorium atau pilot-plant; mengeksplorasi efek dari kondisi operasi yang berbeda untuk studi optimasi dan kontrol; membantu dalam perhitungan skala.
- Desain: mengeksplorasi ukuran dan pengaturan peralatan pemrosesan untuk kinerja dinamis; mempelajari interaksi berbagai bagian dari proses, terutama ketika daur ulang material atau integrasi panas digunakan; mengevaluasi proses alternatif dan struktur kontrol dan strategi; simulasi start-up, shutdown, dan situasi darurat dan prosedur.
- Operasional: mengatasi masalah kontrol dan pemrosesan; membantu dalam start-up dan pelatihan operator; mempelajari dampak dan persyaratan untuk proyek perluasan (penghilangan kemacetan); mengoptimalkan operasi pabrik.
Biasanya jauh lebih murah, lebih aman, dan lebih cepat untuk melakukan jenis studi yang tercantum di atas pada model matematika daripada eksperimental pada unit operasi. Namun keterbatasan kemampuan hitung manusia membuat model matematika membutuhkan bantuan komputer dalam proses perhitungan.
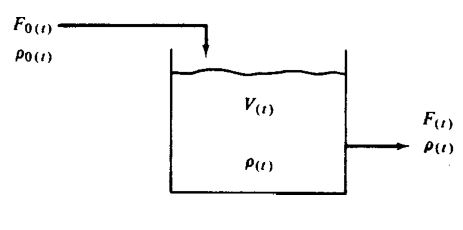
Gambar 2. Matematika model mixed tank [1]
Prinsip Formulasi
Dasar untuk model matematika adalah hukum fisika dan kimia dasar, seperti hukum kekekalan massa, energi, dan momentum. Bentuk umum dengan turunan waktu yang disertakan merupakan ciri khas yang akan selalu ditemui. Sistem deterministik dijelaskan oleh persamaan diferensial biasa hingga parsial. Sebagian besar penekanan akan berada pada sistem yang disamakan (dengan satu variabel independen, waktu, dijelaskan oleh persamaan diferensial biasa). Satuan yang digunakan banyak menggunakan: satuan British dan Satuan Internasional (SI).
Peran vital pemodelan dalam melaksanakan penilaian tekniknya dimulai dari asumsi apa yang dapat dibuat secara sah. Model yang sangat ketat mencakup setiap fenomena hingga detail mikroskopis akan membuatnya menjadi sangat kompleks sehingga akan memakan waktu lama untuk dikembangkan dan mungkin tidak praktis untuk dipecahkan, bahkan pada superkomputer terbaru. Kompromi rekayasa antara deskripsi yang ketat dan mendapatkan jawaban yang cukup baik selalu diperlukan. Hal ini melibatkan asumsi penyederhanaan dengan jumlah yang masuk akal tanpa menghilangkan faktor keutamaan dari analisa yang dicari. Asumsi yang dibuat harus dipertimbangkan dan didaftar dengan hati-hati.
Persamaan model matematika kemudian ditulis, terutama dengan sistem persamaan yang besar dan kompleks, untuk memastikan bahwa jumlah variabel sama dengan jumlah persamaan. Yang disebut “derajat kebebasan” sistem harus nol untuk mendapatkan solusi. Jika hal ini tidak benar, sistem tersebut underspecified atau overspecified sehingga ada yang salah dengan rumusan masalah. Pemeriksaan konsistensi semacam ini mungkin tampak sepele, tetapi dari pengalaman hal itu dapat menghemat berjam-jam dalam berfikir, kebingungan, dan waktu komputer yang terbuang.
Solusi dari persamaan model matematika harus dapat diselesaikan. Teknik dan alat solusi yang tersedia harus dan mampu mengembankan model matematika. Persamaan tanpa cara apa pun untuk menyelesaikannya tidak akan berarti banyak.
Bagian penting tetapi sering diabaikan dalam mengembangkan model matematika adalah membuktikan bahwa model tersebut menggambarkan situasi dunia nyata. Pada tahap desain terkadang hal ini tidak dapat dilakukan karena produk belum dibuat. Namun, bahkan dalam situasi ini biasanya ada produk yang sama atau contoh produk “prototype” dari mana beberapa data dinamis eksperimental dapat diperoleh.
Persamaan Fundamental
1. Persamaan kontinuitas (kekekalan massa)
Prinsip kekekalan massa ketika diterapkan pada sistem dinamis dinyatakan sebagai berikut.
[mass flow masuk sistem] – [mass flow keluar sistem] = [laju perubahan massa di dalam sistem]
2. Persamaan kontinuitas komponen
Tidak seperti massa, komponen kimia tidak kekal. Jika reaksi terjadi di dalam sistem, jumlah mol komponen individu akan meningkat jika itu adalah produk dari reaksi atau berkurang jika itu adalah reaktan. Oleh karena itu persamaan kontinuitas komponen dari spesies kimia sistem dinyatakan sebagai berikut.
[laju mol input sistem] – [laju mol output sistem] + [laju pembentukan mol komponen dari reaksi kimia] = [laju perubahan mol komponen di dalam sistem]
3. Persamaan Energi
Hukum pertama termodinamika mengedepankan prinsip kekekalan energi. Berikut persamaan energi dari aliran masuk dan keluar sistem.
[Energi potensial dari aliran masuk] – [Energi potensial dari aliran keluar] + [Kalor input (konduksi, konveksi, radiasi)] – [Kerja (work)]
= [Energi (internal, kinetik dan potensial) pada laju perubahan sistem]
4. Persamaan gerak (kekekalan momentum)
Persamaan gerak lebih fasih disebut persamaan kekekalan momentum. Di dunia nyata ada tiga arah: x, y, dan z. Tiga keseimbangan gaya dapat ditulis untuk sistem apa pun sehingga setiap sistem memiliki tiga persamaan gerak (ditambah satu keseimbangan massa total, satu persamaan energi, dan keseimbangan komponen).
Alih-alih menulis tiga persamaan gerak, seringkali lebih mudah untuk menulis tiga persamaan sebagai satu persamaan vektor.
5. Persamaan Transport
Hukum transportasi memiliki bentuk fluks (laju transfer per satuan luas) sebanding dengan gaya penggerak (gradien suhu, konsentrasi, atau kecepatan). Konstanta proporsionalitas adalah properti fisik sistem (seperti konduktivitas termal, difusivitas, atau viskositas).
6. Persamaan Kondisi
Persamaan kondisi identik dengan sifat fisik, terutama kepadatan dan entalpi, berubah dengan suhu, tekanan, dan komposisi.
Source:
[1] Luyben, William L. 1996. Process Modelling, Simulation, Control For Chemical Engineers.